PROBABILIDAD Y ESTADÍSTICA

                         PROBABILIDAD Y ESTADÍSTICA

TEORÍA DE CONJUNTOS

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.

Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables ocontradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinito en la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.

Ejemplos.

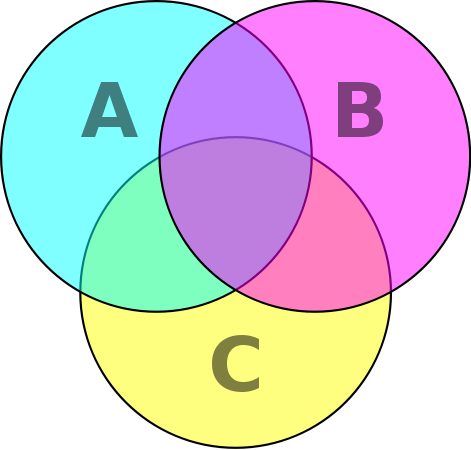
• Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales N, el de los números enteros Z, el de los números racionales Q, el de los números reales Ry el de los números complejos C. Cada uno es subconjunto del siguiente:

• El espacio tridimensional E₃ es un conjunto de objetos elementales denominados puntos p, p ∈ E₃. Las rectas r y planos α son conjuntos de puntos a su vez, y en particular son subconjuntos de E₃, r ⊆ E₃ y α ⊆ E₃.

COMBINACIONES Y PERMUTACIONES

Combinación

Son eventos similares a las permutaciones. Pero el orden ya no importa y es necesario eliminar de las permutaciones aquellas donde los elementos se repiten aunque con distinto orden

Una combinación es una selección de objetos sin importar el orden en que se escojan:

                                                

Permutación

Son eventos de tipo multiplicativo, donde el número de posibilidades va disminuyendo y si importa el orden una permutación es un arreglo de un conjunto de objetos en un orden definido. El número de permutaciones diferentes de estos objetos es ; esto se vé fácilmente si pensamos que para la primera alternativa disponemos de los elementos del conjunto, cada uno de los cuales puede complementarse con los restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto .

El número de permutaciones posibles al tomar objetos del conjunto de elementos será, siguiendo el mismo razonamiento.

                                                       

PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ

Ejemplo : ¿De cuántas formas diferentes se pueden ordenar las letras de la palabraIMPUREZA?

Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:

8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320

PERMUTACIONES CIRCULARES

Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?

Observemos los siguientes arreglos:

Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente .

PERMUTACIONES SIN REPETICIÓN

Ejemplo 7: ¿ De cuántas formas diferentes se pueden sentar seis alumnos en un salón de clases con 25 pupitres?

Solución: El primer estudiante puede elegir entre 25 lugares, el segundo tendrá 24 lugares a escoger, el tercero 23, así sucesivamente; por lo tanto el número de arreglos sin repetición de 25 elementos tomados de 6 en 6 es:

Esto se simboliza por = 

PERMUTACIONES CON REPETICIÓN

Veamos otra aplicación del principio de la multiplicación. Supongamos que tenemos 20 niños de un grupo de Preescolar y 10 sabores de helados disponibles. ¿De cuántas formas diferentes podemos servir un helado a 20 niños?

Al primer niño le podemos servir uno de los 10 sabores, al segundo niño también le podemos servir los 10 sabores, al tercero también, y así sucesivamente. A cada uno de los 20 niños le podemos servir de los 10 sabores, por lo que

= n^r

Observe que r es el número de veces que se repiten los n elementos.

RESUMEN DE LAS PERMUTACIONES

DESCRIPCIÓN	FÓRMULA
Permutaciones sin repetición de n elementos tomados todos a la vez
Permutaciones circulares de n elementos	!
Permutaciones sin repetición de n elementos tomados de r en r, donde r £ n
Permutaciones con repetición de n elementos tomados de r en r
Permutaciones de n elementos de los cuales p1son de un tipo, p2 son de otro tipo, ¼ , pk de otro tipo, donde p1 + p2 + ¼ +pk = n.

CRITERIO DE LA PROBABILIDAD MÁXIMA

Para cada alternativa a_i se determina la probabilidad de que la variable aleatoria que proporciona el resultado tome un valor mayor o igual que una constante K fijada por el decisor: 

y se selecciona aquella alternativa con mayor probabilidad asociada. Por tanto, el criterio de probabilidad máxima puede resumirse de la siguiente forma:

EJEMPLO

Partiendo del ejemplo ilustrativo de decisión bajo riesgo, la siguiente tabla muestra, para cada una de las alternativas, la probabilidad de que el resultado sea mayor o igual que K=10. 

Criterio de probabilidad máxima

	Estados de la Naturaleza
Alternativas	e1	e2	e3	e4	P
a1	11	9	11	8	0.7
a2	8	25	8	11	0.3
a3	8	11	10	11	0.8
Probabilidades	0.2	0.2	0.5	0.1

Para la alternativa a₁, sólo los resultados correspondientes a los estados e₁ y e₃ superan el valor 10, siendo sus probabilidades asociadas 0.2 y 0.5; sumando ambas se obtiene la probabilidad de obtener un resultado mayor o igual que 10 para la alternativa a₁. De manera análoga se determinan las restantes probabilidades. La alternativa óptima según este criterio sería a₃, pues proporciona la probabilidad más alta.