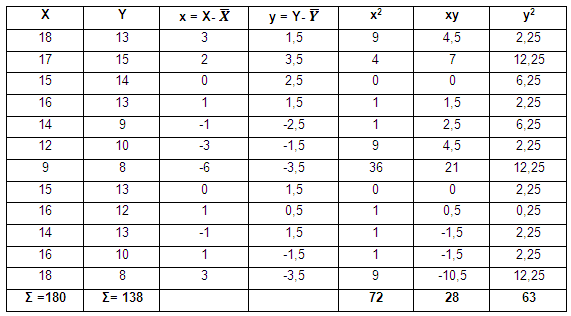
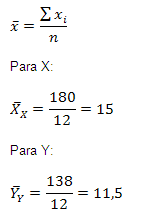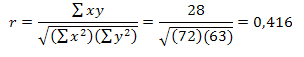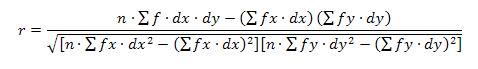ESTADISTICA

martes, 10 de marzo de 2015

CRITERIOS DE PROBABILIDAD

CRITERIOS DE PROBABILIDAD

Para cada alternativa a_ise determina la probabilidad de que la variable aleatoria que proporciona el resultado tome un valor mayor o igual que una constante K fijada por el decisor:

y se selecciona aquella alternativa con mayor probabilidad asociada. Por tanto, el criterio de probabilidad máxima puede resumirse de la siguiente forma:

EJEMPLO

Partiendo del ejemplo ilustrativo de decisión bajo riesgo, la siguiente tabla muestra, para cada una de las alternativas, la probabilidad de que el resultado sea mayor o igual que K=10.

Criterio de probabilidad máxima
	Estados de la Naturaleza
Alternativas	e₁	e₂	e₃	e₄	P
a₁	11	9	11	8	0.7
a₂	8	25	8	11	0.3
a₃	8	11	10	11	0.8
Probabilidades	0.2	0.2	0.5	0.1

Para la alternativa a₁, sólo los resultados correspondientes a los estados e₁ y e₃ superan el valor 10, siendo sus probabilidades asociadas 0.2 y 0.5; sumando ambas se obtiene la probabilidad de obtener un resultado mayor o igual que 10 para la alternativa a₁. De manera análoga se determinan las restantes probabilidades. La alternativa óptima según este criterio sería a₃, pues proporciona la probabilidad más alta.

Probabilidad Simple EJERCICIOS

Problemas resueltos:
Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?

Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:

P(Manzana)=10/30=1/3= 33.3% probable

Calculando igual, la probabilidad de sacar pera es:

P(Pera)=20/30=2/3= 66.7% probable

Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.

2.- la probabilidad de que al lanzar un dado, salga el numero 2 es de

1/6

porque el dos es solo uno de 6 numeros que hay en total.

3.-
En una sala de clases hay 20 mujeres y 12 hombres. Si se escoge uno de ellos al azar. ¿Cuál es la probabilidad de que lapersona escogida sea hombre?
Solución:
Por definición, la probabilidad de que un suceso ocurra viene dada por:
P=casos favorables/casos totales o posibles (P).
En particular, hay 12 hombres, por lo tanto son 12 los casos favorables a dicha selección. Pero ella se hará de un total de 20 + 12 = 32 personas sumamos la cantidad de mujeres y hombres que forman parte de la selección y por tanto, los casos posibles o totales.
Así, la probabilidad pedida es
P= 12/32

4.- En una comida hay 28 hombres y 32 mujeres.Han comido carne 16 hombres y 20 mujeres, comiendo pescado el resto. Si se elige una de las personas al azar. ¿Cuál es la probabilidad de que la persona escogida sea hombre?
Solución:
La información sobre lo que come cada una de las personas es insustancial. Pues en lo que solicita no hay relación con ello. Por definición, la probabilidad pedida viene dada por:
P= casos favorables a la selección 28/casos totales de la muestra 60
P= 28/60

5.-En un curso de 30 alumnos 18 son mujeres. ¿Cuál es la probabilidad de que al escoger una persona está no sea mujer?
Solución:
Claramente nos piden la probabilidad de que al escoger una persona, esta sea hombre. Pues bien, si de los 30 alumnos, 18 son mujeres, entonces hay 12 hombres. Luego, la probabilidad pedida es:
P=casos favorables a la selección 12/casos totales de la muestra 30
P=12/60

Probabilidad conjunta (EJERCICIOS)

EJERCICIOS RESUELTOS:

1.-La probabilidad de sacar dos lápices negros es:

P=(2/5)(1/4)

P=2/20

P= 1/10

2.-En una tómbola hay 3 bolas rojas y 5 blancas. Se extraen unaa una y sin reposición, dos bolas. La probabilidad de que ambas resulten rojas es:

Solución:

Los eventos de extracción son independientes, por lo tanto, la probabilidad pedida

será el producto de cada una de las probabilidades individuales. La 1º extracción tiene 3 casos favorables de untotal de 8 bolas. La probabilidad es 3/8. La 2º tiene 2 casos favorables de un total de7 bolas que quedan. Su probabilidad es 2/7 Así, la probabilidad pedida es

P=(3/8)(2/7)

P=(3/4)(1/7)

P=3/28

3.-Desde una tómbola en la que sólo hay 5 bolitas, 2 negras y 3 rojas, se extraen dos, de una en una y sin reposición. Entonces, la probabilidad de que ambas resulten negras es:

Solución: Los eventos de extracción son independientes, por lo tanto, la probabilidad pedida será el producto de cada una de las probabilidades individuales. La 1º extracción tiene 2 casos favorables de un total de 5 bolas. Su probabilidad es 2/5. La 2º extracción tiene 1 caso favorable de un total de 4 bolas que quedan. Su probabilidad es 1/4 .Así, la probabilidad pedida es

P= (2/5)(1/4)

P= (1/5)(1/2)

P= 1/10

4.-En una urna hay 10 fichas blancas y 5 azules. La probabilidad de que, de dos fichas extraídas una tras otra sin devolución, la primera ficha sea blanca y la segunda sea azul es:

Solución:

Sea B ≡La primera ficha sea blanca.

A ≡La segunda ficha sea azul.

La probabilidad pedida es P (B) •P(A) ,(casos favorables/casos totales), así:

P (B)*P(A)

P= (10/15)(5/14)

P= (5/3) (1/7)

P=5/21

5.-Se extraen dos cartas de una baraja española, una después de la otra sin devolución. La probabilidad que la segunda cartasea un rey, dado que la primera carta fue rey de bastos es:

Solución:

La baraja española consta de 4 reyes en 40 cartas. Después de la 1era extracción quedan 3 reyes en un total de 39 cartas. Entonces, la probabilidad pedida es

P=3/39

P=1/13

Probabilidad de eventos

Regla de Adición

Los eventos compuestos se generan al aplicar las operaciones básicas de los conjuntos a los eventos simples. Las uniones, intersecciones y complementos de eventos son de interés frecuente. La probabilidad de un evento compuesto a menudo pueden obtenerse a partir de las probabilidades de cada uno de los eventos que lo forman. En ocasiones, las operaciones básicas de los conjuntos también son útiles para determinar la probabilidad de un evento compuesto.

De esta manera para A y B eventos del espacio muestral S, entonces:

Demostración:

Se conoce que

por otro lado se tiene que

Entonces

Regla de multiplicación de probabilidades

El siguiente recurso entre material con el que podrás aprender acerca de la Regla de multiplicación de probabilidades, materia de 2° medio.

Regla de multiplicación de probabilidades

1. Regla de multiplicación de probabilidades

Si se tienen varios eventos sucesivos e independientes entre sí, la probabilidad de que ocurran todos ellos a la vez corresponde a la multiplicación de las probabilidades de cada uno de los eventos.

Ejemplos:
1. Si se responden al azar cuatro preguntas con cinco opciones cada una, ¿cuál es la probabilidad de acertar a todas?

La probabilidad de acierto en cada una de las preguntas es 1/5. Por lo tanto, la probabilidad de acertar en las cuatro es:

2. Suponiendo que la probabilidad de tener un hijo o una hija es ½, ¿cuál es la probabilidad de que al tener tres hijos, 2 solamente sean varones?

Si H representa el nacimiento de un hombre y M el de una mujer, tenemos los siguientes casos favorables: HHM – HMH – MHH
La probabilidad de cada uno de estos eventos es:

Ejercicios Resueltos Prob. Total y Teorema de Bayes

EJEMPLO 1

En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.

a. Determine el valor de la probabilidad de que sea menor de 24 meses.

b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.

SOLUCIÓN:

Se definen los sucesos:

Suceso H: seleccionar una niña.

Suceso V: seleccionar un niño.

Suceso M: infante menor de 24 meses.

domingo, 8 de febrero de 2015

PROBABILIDAD Y ESTADÍSTICA

TEORÍA DE CONJUNTOS

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.

Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables ocontradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinito en la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.

Ejemplos.

Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales $N$ , el de los números enteros $Z$ , el de los números racionales $Q$ , el de los números reales $R$ y el de los números complejos $C$ . Cada uno es subconjunto del siguiente:

$\mathbb{N}\subseteq\mathbb{Z}\subseteq\mathbb{Q}\subseteq\mathbb{R}\subseteq\mathbb{C}$

El espacio tridimensional $E 3$ es un conjunto de objetos elementales denominados puntos $p$ , $p \in E 3$ . Las rectas $r$ y planos $α$ son conjuntos de puntos a su vez, y en particular son subconjuntos de $E 3$ , $r \subseteq E 3$ y $α \subseteq E 3$ .

COMBINACIONES Y PERMUTACIONES

Combinación

Son eventos similares a las permutaciones. Pero el orden ya no importa y es necesario eliminar de las permutaciones aquellas donde los elementos se repiten aunque con distinto orden

Una combinación es una selección de objetos sin importar el orden en que se escojan:

Permutación

Son eventos de tipo multiplicativo, donde el número de posibilidades va disminuyendo y si importa el orden una permutación es un arreglo de un conjunto de objetos en un orden definido. El número de permutaciones diferentes de estos objetos es ; esto se vé fácilmente si pensamos que para la primera alternativa disponemos de los elementos del conjunto, cada uno de los cuales puede complementarse con los restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto .

El número de permutaciones posibles al tomar objetos del conjunto de elementos será, siguiendo el mismo razonamiento.

PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ

Ejemplo : ¿De cuántas formas diferentes se pueden ordenar las letras de la palabraIMPUREZA?

Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:

8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320

PERMUTACIONES CIRCULARES

Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?

Observemos los siguientes arreglos:

Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente

PERMUTACIONES SIN REPETICIÓN

Ejemplo 7: ¿ De cuántas formas diferentes se pueden sentar seis alumnos en un salón de clases con 25 pupitres?

Solución: El primer estudiante puede elegir entre 25 lugares, el segundo tendrá 24 lugares a escoger, el tercero 23, así sucesivamente; por lo tanto el número de arreglos sin repetición de 25 elementos tomados de 6 en 6 es:

Esto se simboliza por

PERMUTACIONES CON REPETICIÓN

Veamos otra aplicación del principio de la multiplicación. Supongamos que tenemos 20 niños de un grupo de Preescolar y 10 sabores de helados disponibles. ¿De cuántas formas diferentes podemos servir un helado a 20 niños?

Al primer niño le podemos servir uno de los 10 sabores, al segundo niño también le podemos servir los 10 sabores, al tercero también, y así sucesivamente. A cada uno de los 20 niños le podemos servir de los 10 sabores, por lo que

= n^r

Observe que r es el número de veces que se repiten los n elementos.

RESUMEN DE LAS PERMUTACIONES

*DESCRIPCIÓN*	*FÓRMULA*
Permutaciones sin repetición de n elementos tomados todos a la vez
Permutaciones circulares de n elementos	!
Permutaciones sin repetición de n elementos tomados de r en r, donde r £ n
Permutaciones con repetición de n elementos tomados de r en r
Permutaciones de n elementos de los cuales p₁son de un tipo, p₂ son de otro tipo, ¼ , p_k de otro tipo, donde p₁ + p₂ + ¼ +p_k = n.

CRITERIO DE LA PROBABILIDAD MÁXIMA

Para cada alternativa a_ise determina la probabilidad de que la variable aleatoria que proporciona el resultado tome un valor mayor o igual que una constante K fijada por el decisor:

y se selecciona aquella alternativa con mayor probabilidad asociada. Por tanto, el criterio de probabilidad máxima puede resumirse de la siguiente forma:

EJEMPLO

Partiendo del ejemplo ilustrativo de decisión bajo riesgo, la siguiente tabla muestra, para cada una de las alternativas, la probabilidad de que el resultado sea mayor o igual que K=10.

Criterio de probabilidad máxima
	Estados de la Naturaleza
Alternativas	e₁	e₂	e₃	e₄	P
a₁	11	9	11	8	0.7
a₂	8	25	8	11	0.3
a₃	8	11	10	11	0.8
Probabilidades	0.2	0.2	0.5	0.1

domingo, 23 de noviembre de 2014

Correlación lineal:

En probabilidad y estadística, la correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa

Coeficiente r de Pearson:

El coeficiente de correlación de Pearson se representa con el símbolo ‘r’ , es un índice que mide el grado de covariación entre distintas variables relacionadas linealmente. Esto significa que puede haber variables fuertemente relacionadas, pero no de forma lineal.

Aplicación del coeficiente de correlación de r Pearson

Para interpretar el coeficiente de correlación utilizamos la siguiente escala:

Valor	Significado
-1	Correlación negativa grande y perfecta
-0,9 a -0,99	Correlación negativa muy alta
-0,7 a -0,89	Correlación negativa alta
-0,4 a -0,69	Correlación negativa moderada
-0,2 a -0,39	Correlación negativa baja
-0,01 a -0,19	Correlación negativa muy baja
0	Correlación nula
0,01 a 0,19	Correlación positiva muy baja
0,2 a 0,39	Correlación positiva baja
0,4 a 0,69	Correlación positiva moderada
0,7 a 0,89	Correlación positiva alta
0,9 a 0,99	Correlación positiva muy alta
1	Correlación positiva grande y perfecta

a) Para datos no agrupados se calcula aplicando la siguiente ecuación:

Ejemplo ilustrativo:

Con los datos sobre las temperaturas en dos días diferentes en una ciudad, determinar el tipo de correlación que existe entre ellas mediante el coeficiente de PEARSON.

X	18	17	15	16	14	12	9	15	16	14	16	18	SX =180
Y	13	15	14	13	9	10	8	13	12	13	10	8	SY= 138

Solución:

Se calcula la media aritmética

Se llena la siguiente tabla:

Se aplica la fórmula:

b) Para datos agrupados, el coeficiente de Correlación de Pearson se calcula aplicando la siguiente fórmula:

Donde

n = número de datos.

f = frecuencia de celda.

fx = frecuencia de la variable X.

fy = frecuencia de la variable Y.

dx = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dx = 0, para que se hagan más fáciles los cálculos.

dy = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dy = 0, para que se hagan más fáciles los cálculos.

Ejemplo ilustrativo:

Con los siguientes datos sobre los Coeficientes Intelectuales (X) y de las calificaciones en una prueba de conocimiento (Y) de 50 estudiantes:

N° de estudiante	X	Y	N° de estudiante	X	Y
1	76	28	26	88	40
2	77	24	27	88	31
3	78	18	28	88	35
4	79	41	29	88	26
5	79	43	30	89	30
6	80	45	31	89	24
7	80	34	32	90	18
8	81	18	33	90	11
9	82	40	34	90	15
10	82	35	35	91	38
11	83	30	36	92	34
12	83	21	37	92	31
13	83	22	38	93	33
14	83	23	39	93	35
15	84	25	40	93	24
16	84	11	41	94	40
17	84	15	42	96	35
18	85	31	43	97	36
19	85	35	44	98	40
20	86	26	45	99	33
21	86	30	46	100	51
22	86	24	47	101	54
23	86	16	48	101	55
24	87	20	49	102	41
25	88	36	50	102	45

1) Elaborar una tabla de dos variables

2) Calcular el coeficiente de correlación

Solución:

1) En la tabla de frecuencias de dos variables, cada recuadro de esta tabla se llama una celda y corresponde a un par de intervalos, y el número indicado en cada celda se llama frecuencia de celda. Todos los totales indicados en la última fila y en la última columna se llaman totales marginales o frecuencias marginales, y corresponden, respectivamente, a las frecuencias de intervalo de las distribuciones de frecuencia separadas de la variable X y Y.

Para elaborar la tabla se recomienda:

- Agrupar las variables X y Y en un igual número de intervalos.

- Los intervalos de la variable X se ubican en la parte superior de manera horizontal (fila) y en orden ascendente.

- Los intervalos de la variable Y se ubican en la parte izquierda de manera vertical (columna) y en orden descendente.

Para elaborar los intervalos se procede a realizar los cálculos respectivos:

En la variable X:

En la variable Y:

Recta de regresión por el método de los mínimos cuadrados:

Regresión lineal: El modelo de pronóstico de regresión lineal permite hallar el valor esperado de una variable aleatoria a cuando b toma un valor específico. La aplicación de este método implica un supuesto de linealidad cuando la demanda presenta un comportamiento creciente o decreciente, por tal razón, se hace indispensable que previo a la selección de este método exista un análisis de regresión que determine la intensidad de las relaciones entre las variables que componen el modelo.

Método de los mínimos cuadrados:

Estimación por mínimos cuadrados:

Es el mas utilizado
Fue desarrollado por Karl Gauss (1777-1855)
La idea es producir estimadores de los parámetros ( o, 1) que hagan mínima la suma de cuadrados de las distancias entre los valores observados Yi, y los valores estimados Ŷi 5

Supuestos del método de mínimos cuadrados

1. El modelo de regresión es lineal en los parámetros y
2. Los valores de X son fijos en muestreo repetido.
3. El valor medio de la perturbación i es igual a cero.
4. Homocedasticidad o igual variancia de i.
5. No autocorrelación entre las perturbaciones i.
6. La covariancia entre i y Xi es cero.
7. El número de observaciones n debe ser mayor que el número de parámetros a estimar.
8. Variabilidad en los valores de X.
9. El modelo de regresión está correctamente especificado.
10. No hay relaciones lineales perfectas entre las variables explicativas Xi.

Aplicación de la recta de regresión

Cuadro 1.
Operaciones Mensuales en
una Empresa de Transporte de Pasajeros.

                     Costos      Millas
                    Totales    Vehículo
                     (miles)      (miles)
    Mes Nº          Y              X

        1            213.9        3147
        2            212.6        3160
        3            215.3        3197
        4            215.3        3173
        5            215.4        3292
        6            228.2        3561
        7            245.6        4013
       8            259.9        4244
        9            250.9        4159
      10            234.5        3776
      11            205.9        3232
      12            202.7        3141
      13            198.5        2928
      14            195.6        3063
      15            200.4        3096
      16            200.1        3096
      17            201.5        3158      18            213.2        3338
      19            219.5        3492
      20            243.7        4019
      21            262.3        4394
      22            252.3        4251
      23            224.4        3844
      24            215.3        3276
      25            202.5        3184
      26            200.7        3037
      27            201.8        3142
      28            202.1        3159
      29            200.4        3139
      30            209.3        3203
      31            213.9        3307
      32            227.0        3585
      33            246.4        4073

Fuente: J. Johnston,
Análisis Estadístico de los Costes (Barcelona: Sagitario, S. A., 1966), p. 118.

Como ejemplo, consideremos las cifras del Cuadro 1, que muestra datos mensuales de producción y costos de operación para una empresa británica de transporte de pasajeros por carretera durante los años 1949-52 (la producción se mide en términos de miles de millas-vehículo recorridas por mes, y los costos se miden en términos de miles de libras por mes). Para poder visualizar el grado de relación que existe entre las variables, como primer paso en el análisis es conveniente elaborar undiagrama de dispersión, que es una representación en un sistema de coordenadas cartesianas de los datos numéricos observados. En el diagrama resultante, en el eje X se miden las millas-vehículo recorridas, y en el eje Y se mide el costo de operación mensual. Cada punto en el diagrama muestra la pareja de datos (millas-vehículo y costos de operación) que corresponde a un mes determinado. Como era de esperarse, existe una relación positiva entre estas variables: una mayor cantidad de millas-vehículo recorridas corresponde un mayor nivel de costos de operación.

Por otro lado, también se aprecia por qué este gráfico se denomina un diagrama de "dispersión": no existe una relación matemáticamente exacta entre las variables, ya que no toda la variación en el costo de operación puede ser explicada por la variación en las millas-vehículo. Si entre estas variables existiera una relación lineal perfecta, entonces todos los puntos caerían a lo largo de la recta de regresión, que también ha sido trazada y que muestra la relación "promedio" que existe entre las dos variables. En la práctica, se observa que la mayoría de los puntos no caen directamente sobre la recta, sino que están "dispersos" en torno a ella. Esta dispersión representa la variación en Yque no puede atribuirse a la variación en X.