Correlación lineal:
En probabilidad y estadística, la correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa
Coeficiente r de Pearson:
El coeficiente de correlación de Pearson se representa con el símbolo ‘r’ , es un índice que mide el grado de covariación entre distintas variables relacionadas linealmente. Esto significa que puede haber variables fuertemente relacionadas, pero no de forma lineal.
Aplicación del coeficiente de correlación de r Pearson
Para interpretar el coeficiente de correlación utilizamos la siguiente escala:
Valor
|
Significado
| ||
-1
|
Correlación negativa grande y perfecta
| ||
-0,9 a -0,99
|
Correlación negativa muy alta
| ||
-0,7 a -0,89
|
Correlación negativa alta
| ||
-0,4 a -0,69
|
Correlación negativa moderada
| ||
-0,2 a -0,39
|
Correlación negativa baja
| ||
-0,01 a -0,19
|
Correlación negativa muy baja
| ||
0
|
Correlación nula
| ||
0,01 a 0,19
|
Correlación positiva muy baja
| ||
0,2 a 0,39
|
Correlación positiva baja
| ||
0,4 a 0,69
|
Correlación positiva moderada
| ||
0,7 a 0,89
|
Correlación positiva alta
| ||
0,9 a 0,99
|
Correlación positiva muy alta
| ||
1
|
Correlación positiva grande y perfecta
| ||
a) Para datos no agrupados se calcula aplicando la siguiente ecuación:

Ejemplo ilustrativo:
Con los datos sobre las temperaturas en dos días diferentes en una ciudad, determinar el tipo de correlación que existe entre ellas mediante el coeficiente de PEARSON.
X
|
18
|
17
|
15
|
16
|
14
|
12
|
9
|
15
|
16
|
14
|
16
|
18
|
SX =180
| ||
Y
|
13
|
15
|
14
|
13
|
9
|
10
|
8
|
13
|
12
|
13
|
10
|
8
|
SY= 138
| ||
Solución:
Se calcula la media aritmética
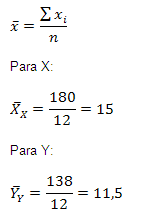
Se llena la siguiente tabla:
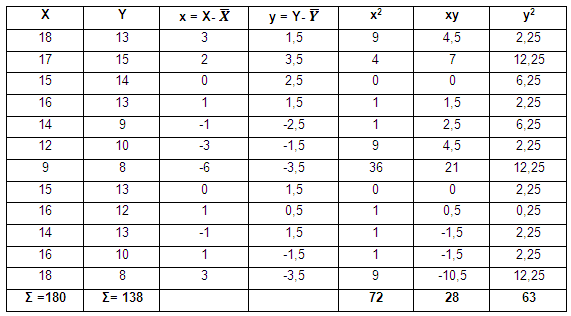
Se aplica la fórmula:
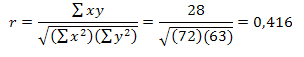
b) Para datos agrupados, el coeficiente de Correlación de Pearson se calcula aplicando la siguiente fórmula:
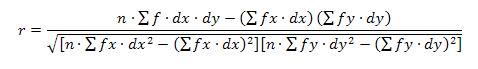
Donde
n = número de datos.
f = frecuencia de celda.
fx = frecuencia de la variable X.
fy = frecuencia de la variable Y.
dx = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dx = 0, para que se hagan más fáciles los cálculos.
dy = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le corresponda dy = 0, para que se hagan más fáciles los cálculos.
Ejemplo ilustrativo:
Con los siguientes datos sobre los Coeficientes Intelectuales (X) y de las calificaciones en una prueba de conocimiento (Y) de 50 estudiantes:
N° de estudiante
|
X
|
Y
|
N° de estudiante
|
X
|
Y
| ||
1
|
76
|
28
|
26
|
88
|
40
| ||
2
|
77
|
24
|
27
|
88
|
31
| ||
3
|
78
|
18
|
28
|
88
|
35
| ||
4
|
79
|
41
|
29
|
88
|
26
| ||
5
|
79
|
43
|
30
|
89
|
30
| ||
6
|
80
|
45
|
31
|
89
|
24
| ||
7
|
80
|
34
|
32
|
90
|
18
| ||
8
|
81
|
18
|
33
|
90
|
11
| ||
9
|
82
|
40
|
34
|
90
|
15
| ||
10
|
82
|
35
|
35
|
91
|
38
| ||
11
|
83
|
30
|
36
|
92
|
34
| ||
12
|
83
|
21
|
37
|
92
|
31
| ||
13
|
83
|
22
|
38
|
93
|
33
| ||
14
|
83
|
23
|
39
|
93
|
35
| ||
15
|
84
|
25
|
40
|
93
|
24
| ||
16
|
84
|
11
|
41
|
94
|
40
| ||
17
|
84
|
15
|
42
|
96
|
35
| ||
18
|
85
|
31
|
43
|
97
|
36
| ||
19
|
85
|
35
|
44
|
98
|
40
| ||
20
|
86
|
26
|
45
|
99
|
33
| ||
21
|
86
|
30
|
46
|
100
|
51
| ||
22
|
86
|
24
|
47
|
101
|
54
| ||
23
|
86
|
16
|
48
|
101
|
55
| ||
24
|
87
|
20
|
49
|
102
|
41
| ||
25
|
88
|
36
|
50
|
102
|
45
| ||
1) Elaborar una tabla de dos variables
2) Calcular el coeficiente de correlación
Solución:
1) En la tabla de frecuencias de dos variables, cada recuadro de esta tabla se llama una celda y corresponde a un par de intervalos, y el número indicado en cada celda se llama frecuencia de celda. Todos los totales indicados en la última fila y en la última columna se llaman totales marginales o frecuencias marginales, y corresponden, respectivamente, a las frecuencias de intervalo de las distribuciones de frecuencia separadas de la variable X y Y.
Para elaborar la tabla se recomienda:
- Agrupar las variables X y Y en un igual número de intervalos.
- Los intervalos de la variable X se ubican en la parte superior de manera horizontal (fila) y en orden ascendente.
- Los intervalos de la variable Y se ubican en la parte izquierda de manera vertical (columna) y en orden descendente.
Para elaborar los intervalos se procede a realizar los cálculos respectivos:
En la variable X:

En la variable Y:

Recta de regresión por el método de los mínimos cuadrados:
Regresión lineal: El modelo de pronóstico de regresión lineal permite hallar el valor esperado de una variable aleatoria a cuando b toma un valor específico. La aplicación de este método implica un supuesto de linealidad cuando la demanda presenta un comportamiento creciente o decreciente, por tal razón, se hace indispensable que previo a la selección de este método exista un análisis de regresión que determine la intensidad de las relaciones entre las variables que componen el modelo.
Método de los mínimos cuadrados:
Estimación por mínimos cuadrados:
- Es el mas utilizado
- Fue desarrollado por Karl Gauss (1777-1855)
- La idea es producir estimadores de los parámetros ( o, 1) que hagan mínima la suma de cuadrados de las distancias entre los valores observados Yi, y los valores estimados Ŷi 5
- 1. El modelo de regresión es lineal en los parámetros y
- 2. Los valores de X son fijos en muestreo repetido.
- 3. El valor medio de la perturbación i es igual a cero.
- 4. Homocedasticidad o igual variancia de i.
- 5. No autocorrelación entre las perturbaciones i.
- 6. La covariancia entre i y Xi es cero.
- 7. El número de observaciones n debe ser mayor que el número de parámetros a estimar.
- 8. Variabilidad en los valores de X.
- 9. El modelo de regresión está correctamente especificado.
- 10. No hay relaciones lineales perfectas entre las variables explicativas Xi.
Aplicación de la recta de regresión
Cuadro 1.
Operaciones Mensuales en una Empresa de Transporte de Pasajeros.
Costos Millas
Totales Vehículo (miles) (miles) Mes Nº Y X 1 213.9 3147 2 212.6 3160 3 215.3 3197 4 215.3 3173 5 215.4 3292 6 228.2 3561 7 245.6 4013 8 259.9 4244 9 250.9 4159 10 234.5 3776 11 205.9 3232 12 202.7 3141 13 198.5 2928 14 195.6 3063 15 200.4 3096 16 200.1 3096 17 201.5 3158 18 213.2 3338 19 219.5 3492 20 243.7 4019 21 262.3 4394 22 252.3 4251 23 224.4 3844 24 215.3 3276 25 202.5 3184 26 200.7 3037 27 201.8 3142 28 202.1 3159 29 200.4 3139 30 209.3 3203 31 213.9 3307 32 227.0 3585 33 246.4 4073 Fuente: J. Johnston, Análisis Estadístico de los Costes (Barcelona: Sagitario, S. A., 1966), p. 118. |
Como ejemplo, consideremos las cifras del Cuadro 1, que muestra datos mensuales de producción y costos de operación para una empresa británica de transporte de pasajeros por carretera durante los años 1949-52 (la producción se mide en términos de miles de millas-vehículo recorridas por mes, y los costos se miden en términos de miles de libras por mes). Para poder visualizar el grado de relación que existe entre las variables, como primer paso en el análisis es conveniente elaborar undiagrama de dispersión, que es una representación en un sistema de coordenadas cartesianas de los datos numéricos observados. En el diagrama resultante, en el eje X se miden las millas-vehículo recorridas, y en el eje Y se mide el costo de operación mensual. Cada punto en el diagrama muestra la pareja de datos (millas-vehículo y costos de operación) que corresponde a un mes determinado. Como era de esperarse, existe una relación positiva entre estas variables: una mayor cantidad de millas-vehículo recorridas corresponde un mayor nivel de costos de operación.
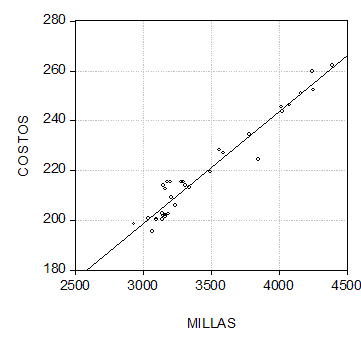
Por otro lado, también se aprecia por qué este gráfico se denomina un diagrama de "dispersión": no existe una relación matemáticamente exacta entre las variables, ya que no toda la variación en el costo de operación puede ser explicada por la variación en las millas-vehículo. Si entre estas variables existiera una relación lineal perfecta, entonces todos los puntos caerían a lo largo de la recta de regresión, que también ha sido trazada y que muestra la relación "promedio" que existe entre las dos variables. En la práctica, se observa que la mayoría de los puntos no caen directamente sobre la recta, sino que están "dispersos" en torno a ella. Esta dispersión representa la variación en Yque no puede atribuirse a la variación en X.
No hay comentarios:
Publicar un comentario